El número phi, también conocido como la proporción áurea o la divina proporción, es un concepto matemático que ha fascinado a matemáticos, artistas, arquitectos y científicos durante siglos. Representado por la letra griega φ (phi), su valor aproximado es 1.6180339887… y se encuentra en la intersección de las matemáticas, la naturaleza y el arte. En este ensayo exploraremos su origen, sus propiedades matemáticas, su presencia en la naturaleza y su influencia en el arte y la arquitectura.
El origen del número phi
El concepto de la proporción áurea tiene sus raíces en la Antigua Grecia, donde los matemáticos estudiaron la geometría y descubrieron relaciones proporcionales que parecían tener cualidades estéticamente agradables. Euclides, en su obra Elementos, describió una división en “extrema y media razón”, que es esencialmente una definición temprana de lo que hoy llamamos la proporción áurea. El término “phi” fue asignado mucho más tarde, en honor al escultor griego Fidias, quien supuestamente utilizó esta proporción en sus obras.
Propiedades matemáticas
La proporción áurea surge de la solución de la ecuación cuadrática:
$$ x^2 – x – 1 = 0 $$
La solución positiva de esta ecuación es el valor de phi:
$$ \phi = \frac{1+\sqrt{5}}{2} $$
Entre sus propiedades matemáticas más notables está su relación con la sucesión de Fibonacci. Al dividir un número de Fibonacci por el anterior en la sucesión, el cociente se aproxima cada vez más a phi a medida que los números crecen. Además, phi tiene propiedades geométricas únicas: un rectángulo áureo, al dividirse en un cuadrado y otro rectángulo, genera un nuevo rectángulo cuyas proporciones también son áureas.
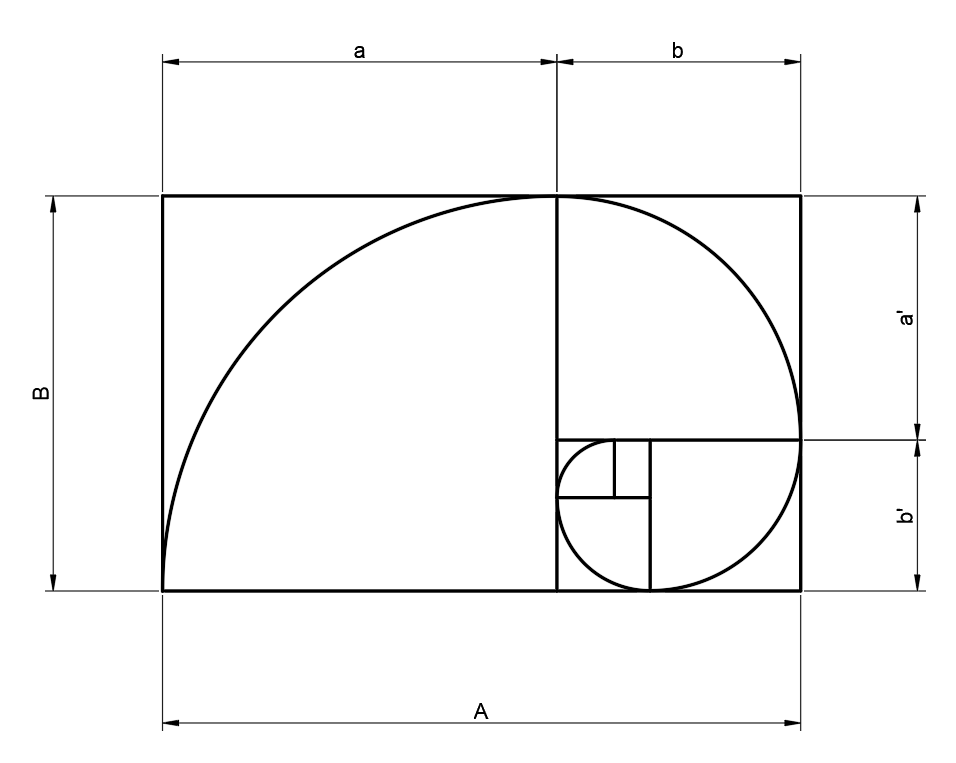
La espiral áurea o espiral de Fibonacci surge a partie de un rectángulo cuyas proporciones son la razón aurea, es decir, que la relación entre A y B es Phi. Asimismo en cada ciclo de la espiral se cumple la misma proporción es decir entre a y b, y entre a’ y b’, y así sucesivamente.
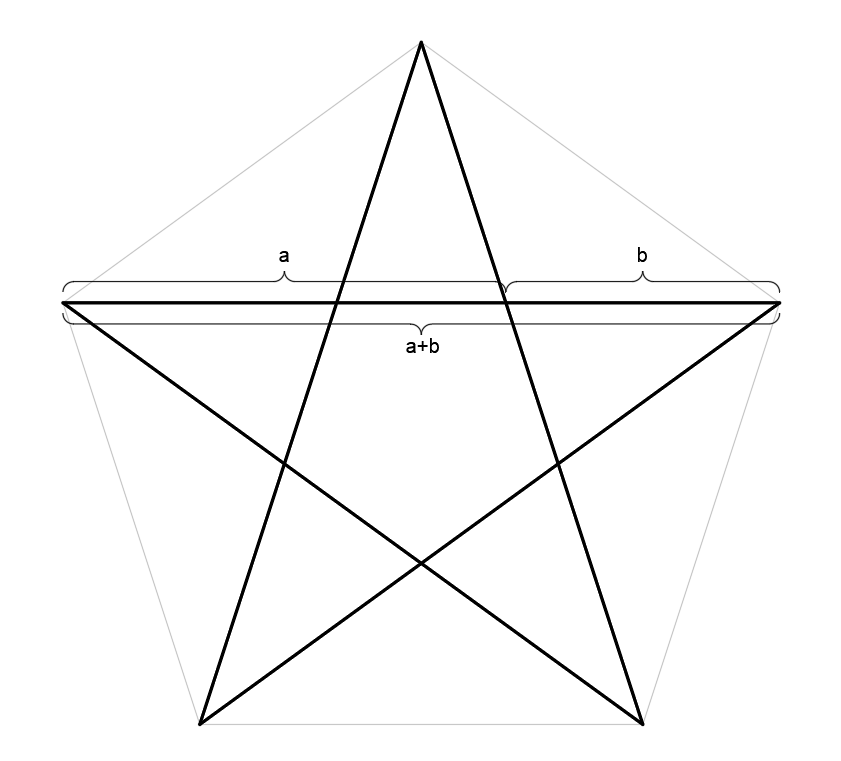
Otro ejemplo es el pentagrama, la estrella que sale de unir los vértices de un pentágono. La relación entre (a+b) con a es Phi, también la relación de a con b.
Phi en la naturaleza
La proporción áurea se manifiesta de manera asombrosa en la naturaleza. Un ejemplo común es la disposición de las hojas en los tallos de las plantas, conocida como filotaxis, que optimiza la captación de luz solar. También aparece en las espirales de las piñas, los girasoles y las conchas de los nautilos. Estas formas naturales reflejan una organización basada en la eficiencia y la armonía, características que también se atribuyen a la proporción áurea.
Phi en el arte y la arquitectura
El uso de la proporción áurea en el arte y la arquitectura es legendario. Se cree que los antiguos egipcios la emplearon en el diseño de las pirámides de Giza, y que los griegos la incorporaron en el Partenón. Durante el Renacimiento, artistas como Leonardo da Vinci exploraron la proporción áurea en sus obras. El “Hombre de Vitruvio” es un ejemplo famoso, ya que ilustra las proporciones ideales del cuerpo humano en relación con phi.
En la arquitectura moderna, también se han utilizado las proporciones áureas para crear estructuras equilibradas y agradables a la vista. Ejemplos incluyen obras de Le Corbusier, quien desarrolló un sistema de proporciones basado en phi llamado “Modulor”.
Conclusión
El número phi, o la divina proporción, es un testimonio de la conexión intrínseca entre las matemáticas, la naturaleza y la creatividad humana. Su presencia en el mundo natural y su influencia en el arte y la arquitectura subrayan su papel como una de las ideas matemáticas más fascinantes. Al estudiar phi, no solo apreciamos una proporción estética, sino también una puerta hacia una comprensión más profunda de la armonía universal.
